Early last month, I was chatting with one of my officemates about a curious problem I had studied in high school. I hadn't written any of the results down, so much of the discussion involved me rediscovering the results and proving them with much more powerful tools than I once possessed.

Before writing about the problem I had played around with, I want to give a brief motivation. For as long as humans have been doing mathematics, finding values of $\pi$ has been deemed worthwhile (or every generation has just found it worthwhile to waste time computing digits).

One such way the Greeks (particularly Archimedes) computed $\pi$ was by approximating a circle by a regular polygon and letting the number of sides grow large enough so that the error between the area of the unit circle $(\pi \cdot 1^2)$ and the area of the polygon would be smaller than some fixed threshold. Usually these thresholds were picked to ensure that the first $k$ digits were fully accurate — for some appropriate value of $k$.

In many introductory Calculus courses, this problem is introduced exactly when the limit is introduced and students are forced to think about the area problem in the regular polygon:

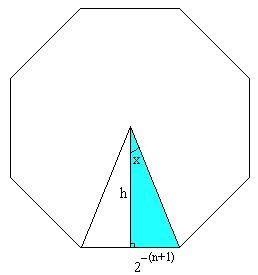
Given $N$ sides, the area is $N \cdot T_N$ where $T_N$ is the area of each individual triangle given by one side of the polygon and the circumcenter.

Call one such triangle $\Delta ABC$ and let $BC$ be the side that is also a side of the polygon while the other sides have $\left|AB\right| = \left|AC\right| = 1$ since the polygon is inscribed in a unit circle. The angle $\angle BAC = \frac{2\pi}{N}$ since each of the triangles has the same internal angle and there are $N$ of them. If we can find the perpendicular height $h$ from $AB$ to $C,$ the area will be $\frac{1}{2} h \left|AB\right| = \frac{h}{2}$. But we also know that

hence

Combining all of these, we can approximate $\pi$ with the area:

As I've shown my Math 1A students, we see that

so these are indeed good approximations.

Theory is Nice, But I Thought We Were Computing Something

Unfortunately for us (and Archimedes), computing $\sin\left(\frac{2\pi}{N}\right)$ is not quite as simple as dividing by $N,$ so often special values of $N$ were chosen. In fact, starting from $N$ and then using $2N,$ the areas could be computed via a special way of averaging the previous areas. Lucky for us, such a method is equivalent to the trusty half angle identities (courtesy of Abraham De Moivre). To keep track of these polygons with a power of two as the number of sides, we call

Starting out with the simplest polygon, the square with $N = 2^2$ sides, we have

Jumping to the octagon (no not that "The Octagon"), we have

So far, the toughest thing we've had to deal with is a $45^{\circ}$ angle and haven't yet had to lean on Abraham (him, not him) for help. The hexadecagon wants to change that:

To really drill home the point (and motivate my next post) we'll compute this for the $32$-gon (past the point where polygons have worthwhile names):

Before, we could rely on the fact that we know that a 45-45-90 triangle looked like, but now, we come across $\cos\left(\frac{\pi}{8}\right),$ a value which we haven't seen before. Luckily, Abraham has help here as well:

which lets us compute

So why have I put you through all this? If we wave our hands like a magician, we can see this pattern continues and for the general $n$

where there are $n - 3$ nested radicals with the $\oplus$ sign and only one minus sign at the beginning.

This motivates us to study two questions, what is the limiting behavior of such a nested radical:

as the signs $s_1, s_2, \ldots$ take values in $\left\{-1, 1\right\}$. Recasting in terms of the discussion above, we want to know how close we are to $\pi$ as we increase the number of sides.

When I was in high school, I just loved to nerd out on any and all math problems, so I studied this just for fun. Having heard about the unfathomable brain of Ramanujan and the fun work he had done with infinitely nested radicals, I wanted to examine which sequences of signs

produced an infinite radical that converged and what the convergence behavior was.

I'm fairly certain my original questions came from an Illinois Council of Teachers of Mathematics (ICTM) contest problem along the lines of

or maybe the slightly more difficult

Armed with my TI-83, I set out to do some hardcore programming and figure it out. It took me around a month of off-and-on tinkering. This second time around as a mathematical grown-up, it took me the first half of a plane ride from SFO to Dallas.

In the next few weeks/months, I hope to write a few blog posts, including math, proofs and some real code on what answers I came up with and what other questions I have.