Below, we'll show two facts which help understand the positive integer solutions to the following diophantine equation:

We'll show that there is a lone positive root and as $m \longrightarrow \infty$ the root approaches:

Additionally, if this root is an integer (i.e. the relevant solutions to a diophantine equation), then for $m \geq 4$ it must be exactly equal to:

Contents

• Motivation
• Open Question
• Reframing
• Finding Coefficients
• Root as Floor
• Tighter Bounds
• Future Work

Motivation

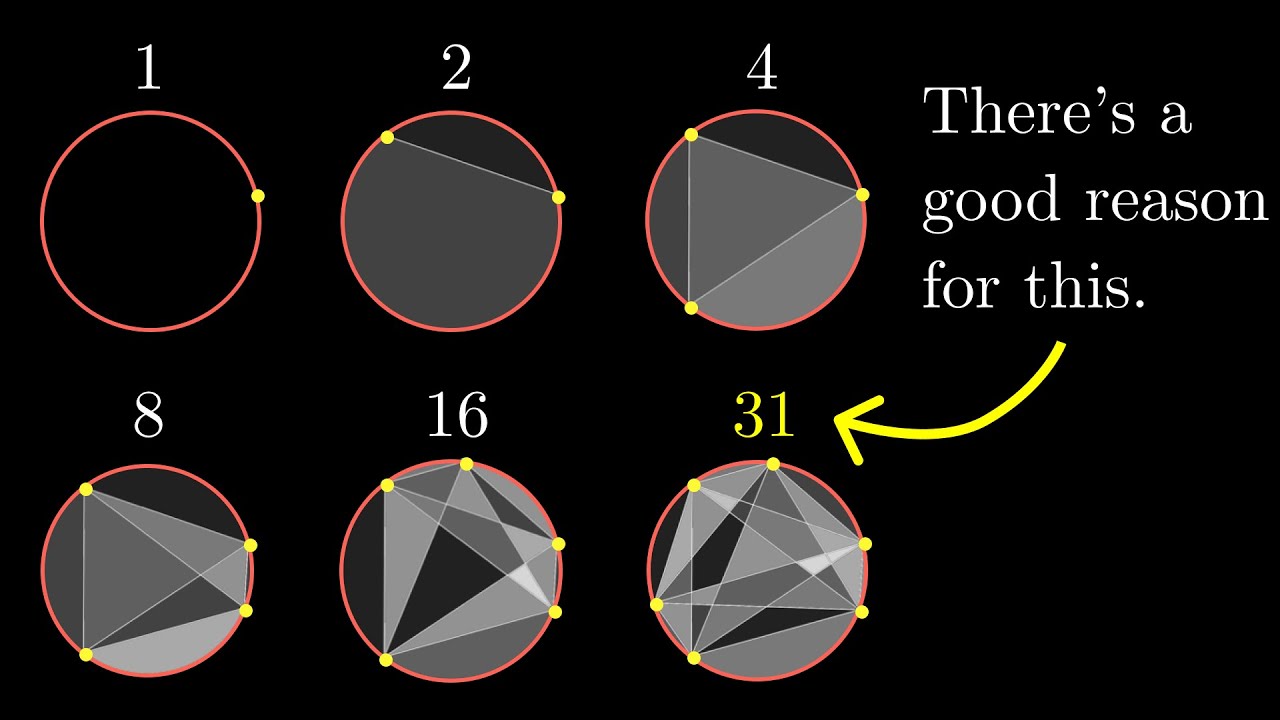
I started down this path after watching a video from 3Blue1Brown¹ where he discusses Moser's circle problem. In particular, he demonstrates the formula

for the number of distinct regions a circle is divided into when connecting all pairs of $n$ points around the circle in general position.

The video is about showing the perils of assuming a pattern repeats indefinitely:

but also shows one more value equal to a power of two: $F_{10} = 256$.

Open Question

At the end of the video he poses a challenge question that piqued my interest and that's what we'll be talking about here²: Will there ever be another power of 2?

There is a fairly clean solution to this on Math StackExchange, but it uses extremely non-elementary methods (I am not a number theorist). It does use a simple observation to transform the exponential part of the equation into a low degree polynomial so that existing tools for solving diophantine equations can be used. In particular, it uses the observation that $2^m$ is either equal to $k^2$ or $2k^2$ depending on the parity of $m$.

I tried (and failed) to make progress on this challenge question by investigating properties of a solution $n$ as $m$ varies. (As opposed to what I view the more common approach of investigating factors of $F_n$ as $n$ varies.) However along the way I discovered some interesting facts about the roots as $m \longrightarrow \infty$.

Reframing

We'll reframe $F_n = 2^m$ via a change of variables to get an explicit Laurent series to more easily understand the behavior of the positive root. Note that we can say the positive root: there is exactly one. To see why, consider

This function is concave up since monic and

For $m \geq 1$ we have $f(0; m) = f(1; m) = -24\left(2^m - 1\right) < 0$ which guarantees a root greater than 1 and a root less than 0.

We'd like to understand the asymptotic root behavior, but as $m \longrightarrow \infty$ both the "input" $2^m$ goes to infinity and the "output" $n$ goes to infinity since the largest term of the polynomial will dominate:

We'd like a Taylor series at infinity that converges to infinity. However, no such expansion exists, so we instead use a quantity that goes to infinity as some input $X$ goes to zero:

This satisfies $\frac{1}{X^4} \longrightarrow \infty$ as $X \longrightarrow 0^+$ but since $n \sim \sqrt[4]{\frac{1}{X^4}} = \frac{1}{X}$ it doesn't solve the $n \longrightarrow \infty$ problem. For that, we use the substitution $s = n X$ and now can start to pursue a Taylor series for our root via

which is equivalent to finding roots of the parameterized polynomial

This polynomial allows us to define the positive root $\alpha(X)$ as an implicit function via

We'll start from the Taylor series

and transform to the Laurent series for $n = s / X$

Finding Coefficients

To find the first few terms of this expansion, we'll utilize SymPy. First, we'll set up our variables, our parameterized polynomial $g(s; X)$ and the first three terms of the Taylor series $\alpha(X)$ (utilizing the very useful sympy.Order type in SymPy):

In [1]: import sympy; sympy.__version__
Out[1]: '1.12'

In [2]: a0, a1, a2, s, X = sympy.symbols("a0, a1, a2, s, X")

In [3]: g = s**4 - 6 * X * s**3 + 23 * X**2 * s**2 - 18 * X**3 * s + (24 * X**4 - 1)

In [4]: alpha = a0 + a1 * X + a2 / 2 * X**2 + sympy.Order(X**3)

Substituting alpha and expanding, we have a series with quadratic terms in $X$ and as expected a tail of the form $\mathcal{O}\left(X^3\right)$:

In [5]: g.subs({s: alpha}).expand()
Out[5]: -1 + a0**4 - 6*X*a0**3 + 4*X*a0**3*a1 + 23*X**2*a0**2 - 18*X**2*a0**2*a1 + 6*X**2*a0**2*a1**2 + 2*X**2*a0**3*a2 + O(X**3)

In [6]: T2 = sympy.Poly(g.subs({s: alpha}).expand().removeO(), X)

In [7]: T2
Out[7]: Poly((2*a0**3*a2 + 6*a0**2*a1**2 - 18*a0**2*a1 + 23*a0**2)*X**2 + (4*a0**3*a1 - 6*a0**3)*X + a0**4 - 1, X, domain='ZZ[a0,a1,a2]')

Setting the coefficients of the first three terms to zero, we'll have our expansion:

In [8]: T2.coeff_monomial(1)
Out[8]: a0**4 - 1

In [9]: T2.coeff_monomial(X).factor()
Out[9]: 2*a0**3*(2*a1 - 3)

In [10]: T2.coeff_monomial(X**2).factor()
Out[10]: a0**2*(2*a0*a2 + 6*a1**2 - 18*a1 + 23)

Since we want the positive root, we choose $\alpha(0) = a_0 = 1$. Independent of this value we also see $a_1 = \frac{3}{2}$ (since all four possible values of $a_0$ are nonzero). Finally solving for the last term:

In [11]: T2.coeff_monomial(X**2).subs({a0: 1, a1: sympy.Rational(3, 2)}).factor()
Out[11]: (4*a2 + 19)/2

Putting it all together:

Root as Floor

We'll show below that $1 + \frac{1}{2} X < \alpha(X) < 1 + \frac{3}{2} X$ for small enough $X$³. Once established, this means

and since this interval has a width of $1$ we have $n = \left\lfloor \frac{1}{X} + \frac{3}{2} \right\rfloor$. The connection to $m$ comes in via:

We can establish the upper bound via:

This quantity is always positive for $X$ in our domain, which means it is to the right of $\alpha(X)$ due to the concavity of $g$.

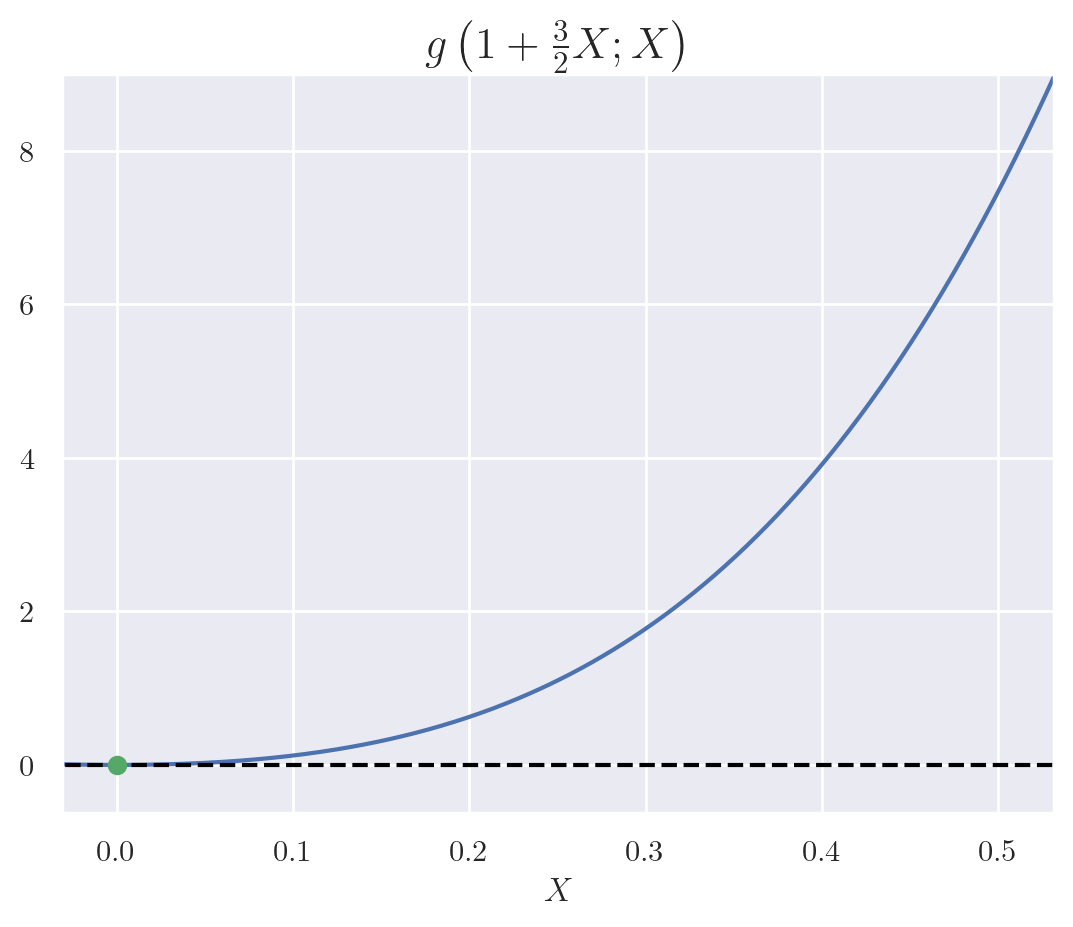
For the lower bound:

This quantity is negative for $X < 0.2371$ which first happens when $m = 4$ and remains negative thereafter:

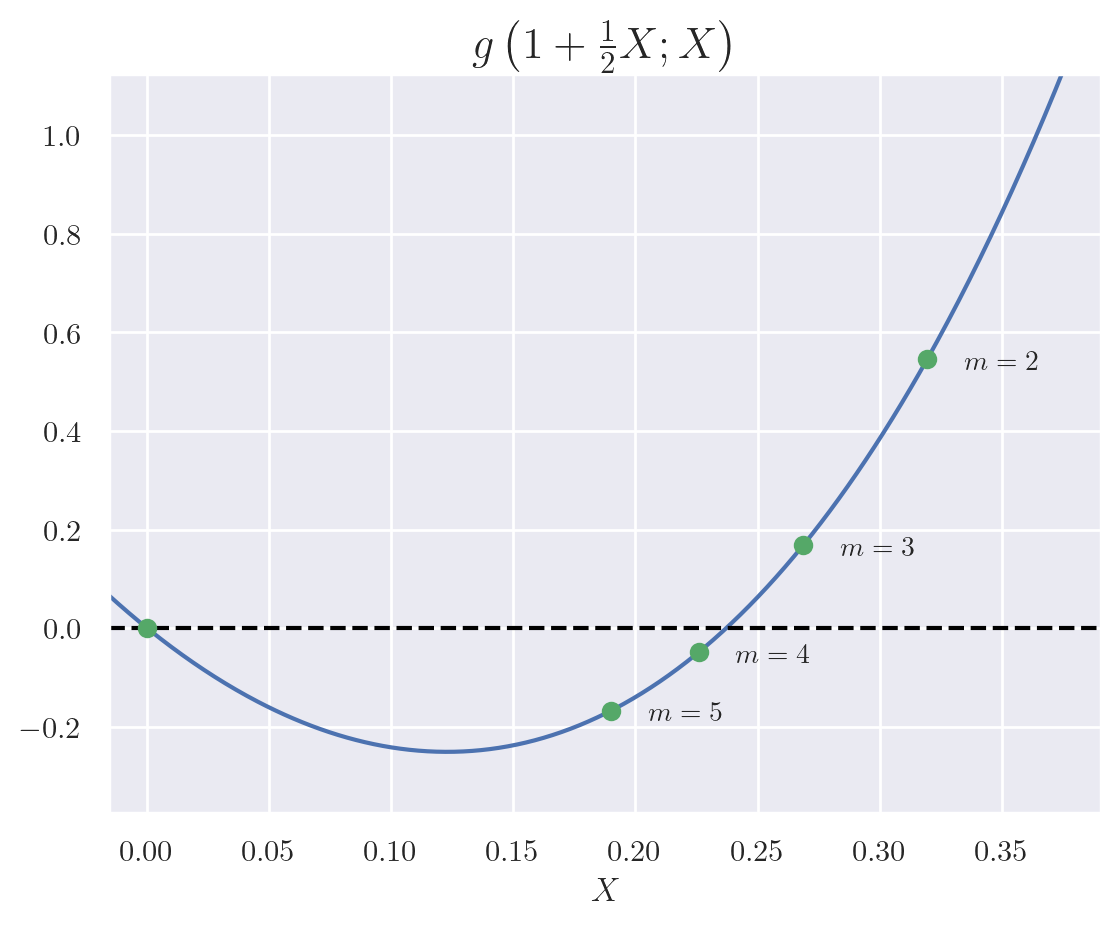
Tighter Bounds

In an attempt to show that there could be no more solutions to the original diophantine equation, I tightened the bounds on $\alpha(X)$ and explored the behavior. In fact, for $m \geq 20$ we have

which is a very small window of width $0.04$. I was hoping to show that for large enough $m$ this window contains no integers,= but unfortunately it appears that the window contains an integer about 4% of the time. Plotting the number of such windows $C_{1.46}(m)$ against a line with slope $0.04$:

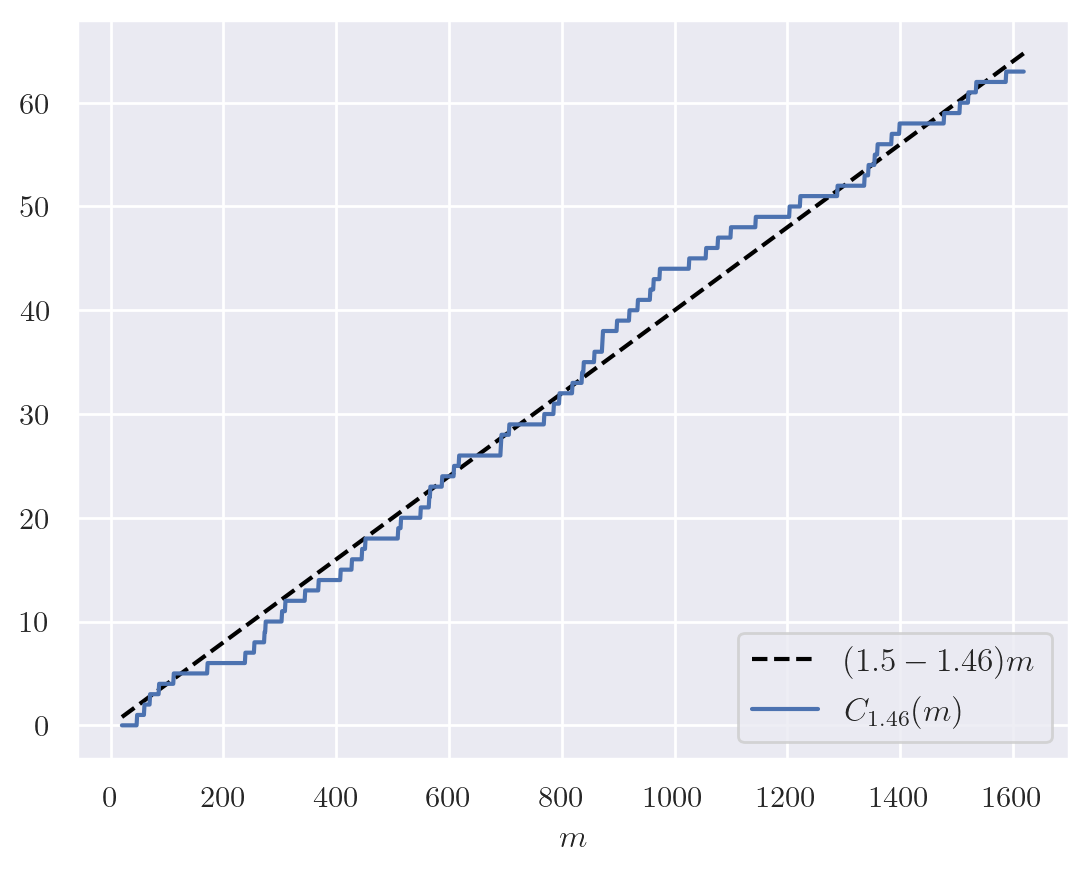
Future Work

Though I didn't get the result I was hoping for, I did have a lot of fun exploring the behavior of roots as $m \longrightarrow \infty$. I do think there is more progress to be made in this direction. For example, in order for our expected root to actually be a root, we must have

but it appears that $m = 36$ is the last time this is satisfied.

1. Grant Sanderson, aka 3Blue1Brown is awesome and I highly recommend all of his videos. ↩
2. I know the last time I wrote about math on this blog it was the same situation, i.e. an offhand comment on a popular YouTube video. ↩
3. Note that the negative quadratic term in the Taylor series for the root indicates the upper bound. ↩