About a year ago, I was reading the Go source for computing $\log(x)$ and was very surprised by the implementation.¹

Even three years into a PhD in Applied Math (i.e. numerics), I still managed to learn something by diving in and trying to understand what was going on.

(Almost-)Correctness

Really I just wanted a chance to share a neat error plot:

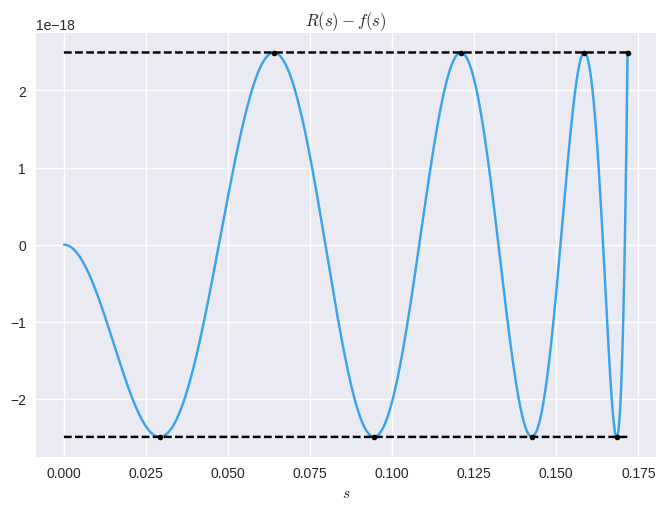
The high-level:

• The computation $\log(x)$ can be reduced to computing a related function $R(s)$ (where the value $s$ can be obtained from $x$ on a computer in some straightforward way)
• $R(s)$ can be approximated by a function that we can actually compute with simple floating point operations: $f(s)$
• The error $R(s) - f(s)$ is "equioscillating", i.e. it minimizes the maximum error, a so-called minimax solution

If you're still interested in some mathematical details, stick around. If not, I hope you enjoyed the pretty picture.

Doing the Obvious

The "obvious" idea that comes to mind is to use a Taylor series approximation. But $\log(x)$ is not defined at $x = 0,$ so a Taylor series of a related function is typically used²:

But, the implementation doesn't do the obvious thing. Instead it breaks down the argument into an exponent and a fractional part

which transforms the computation to:

The first part $k \log(2)$ can be handled in maximal precision for the limited set of integer values that $k$ can be.

Finding a Function to Approximate

For the other part

From here, I expected a polynomial approximation that just takes the first few terms in $R(s)$. However, coefficients that are close (but not equal) are given:

L1    = 6.666666666666735130e-01   /* 3FE55555 55555593 */
L2    = 3.999999999940941908e-01   /* 3FD99999 9997FA04 */
L3    = 2.857142874366239149e-01   /* 3FD24924 94229359 */
L4    = 2.222219843214978396e-01   /* 3FCC71C5 1D8E78AF */
L5    = 1.818357216161805012e-01   /* 3FC74664 96CB03DE */
L6    = 1.531383769920937332e-01   /* 3FC39A09 D078C69F */
L7    = 1.479819860511658591e-01   /* 3FC2F112 DF3E5244 */

For example:

Not Go, Sun

You may have noted my typo above: I used $R(z)$ when I should've used $R(s)$. This typo is directly from the source; not my copy-paste error, but a copy-paste error in the original source.

The original authors aren't the Golang devs:

// The original C code, the long comment, and the constants
// below are from FreeBSD's /usr/src/lib/msun/src/e_log.c
// and came with this notice. The go code is a simpler
// version of the original C.

It seems they copied everything, even the typos. Another typo can be found when the description mentions "a special Reme algorithm" used to compute the coefficients $L_j$.

This typo is a bit more egregious: it actually uses a Remez algorithm.

Remez Algorithm

This algorithm takes a polynomial approximation like

and systematically modifies the coefficients until the error is "equioscillating":

Is That All You've Got?

I hope to follow this post up with some code to actually compute the coefficients that give an equioscillating error (and to show some coefficients that do slightly better).

1. Why would anyone look in this source? I was trying to explain to a student that a computer would compute this with minimal error when I realized I didn't know how. ↩
2. This series is typically learned and forgotten by those who have made it through "Calc II". ↩