I enjoy watching math videos targeted at advanced high school or undergraduate students — even if the topics are far away from research level mathematics. I was recently watching a "quick and easy challenge in algebra" video from SyberMath1 that used a neat trick to solve the problem. As the video title hints, this could've been a homework problem for advanced high schoolers. In the video, SyberMath makes an offhand comment:
Notice that the original expression is equal to one and obviously you can find some numbers that satisfy this, right?
The ensuing proof in the video shows that an identity holds for all values, so the task of "find some numbers" never actually happens. However, this comment stuck with me and I tried to find the "simplest" numbers that would make that expression equal one. Going down this path I accidentally waded2 into deep waters with advanced number theory concepts.
Contents
Original Problem
The original problem statement3 is as follows. Given
show:
This blog post will focus on finding triples that satisfy the first equation. I was hoping I could find a solution in but as we'll see below this is impossible!
Reduction
TL;DR we reduce to two degrees of freedom via
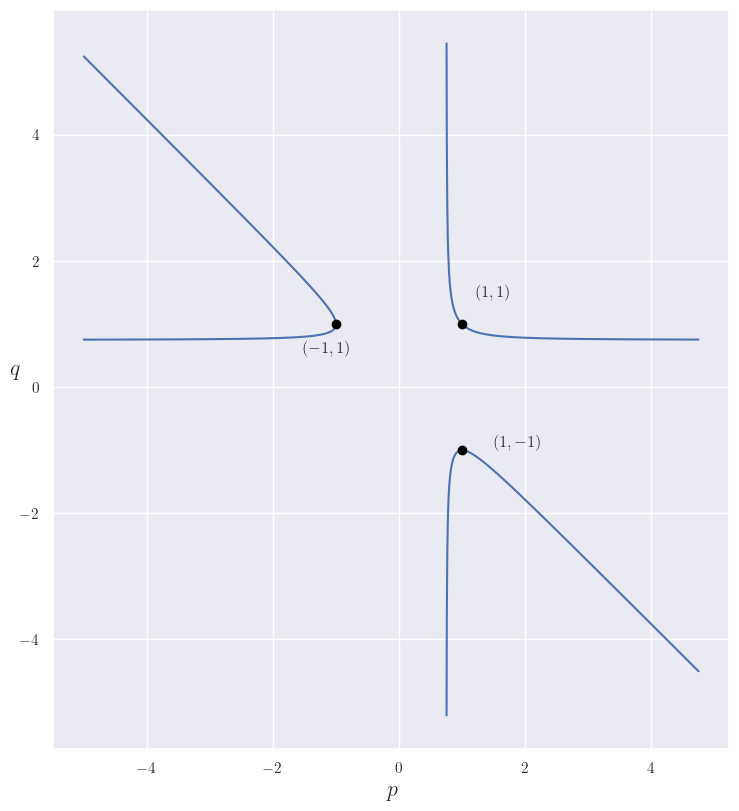
Feel free to skip to the next section if you don't care how or why we can make this reduction.
Since the equation has three unknowns and one constraint, we expect the solution to be a family with two degrees of freedom, so we want to first reduce it. Note that this equation is homogeneous; scaling to for any will preserve the relationship.
For the expression to be well-defined we must have (and similar for the other permuted denominators). With this out of the way we'll incorporate into the original equation in a fashion similar to the trick in the video:
We must have and by symmetry and . By way of contradiction, if :
which can't happen since . Using this, we can finally show ; again by way of contradiction, if :
Now we can safely divide by to make an equation with our two free parameters:
A Wild Elliptic Curve Appears
Clearing denominators in our equation we can form a quadratic in :
which has solutions:
Given a rational we only have rational if the discriminant is the square of a rational:
Thanks to a helpful tip to use a Möbius transformation, we can transform via
which produces an elliptic curve in Weierstrass form:
In other words, rational solutions correspond to rational solutions which in turn correspond to rational points on this elliptic curve.
Bad News
In general, finding rational points on an elliptic curve (and proving you have found them all) is a challenge. Luckily MAGMA exists and the helpful mathematicians on the internet want you to know. Plugging in our curve
E:=EllipticCurve([215 / 3, - 10582 / 27]);
MordellWeilGroup(E);
RationalPoints(E : Bound:=1000);
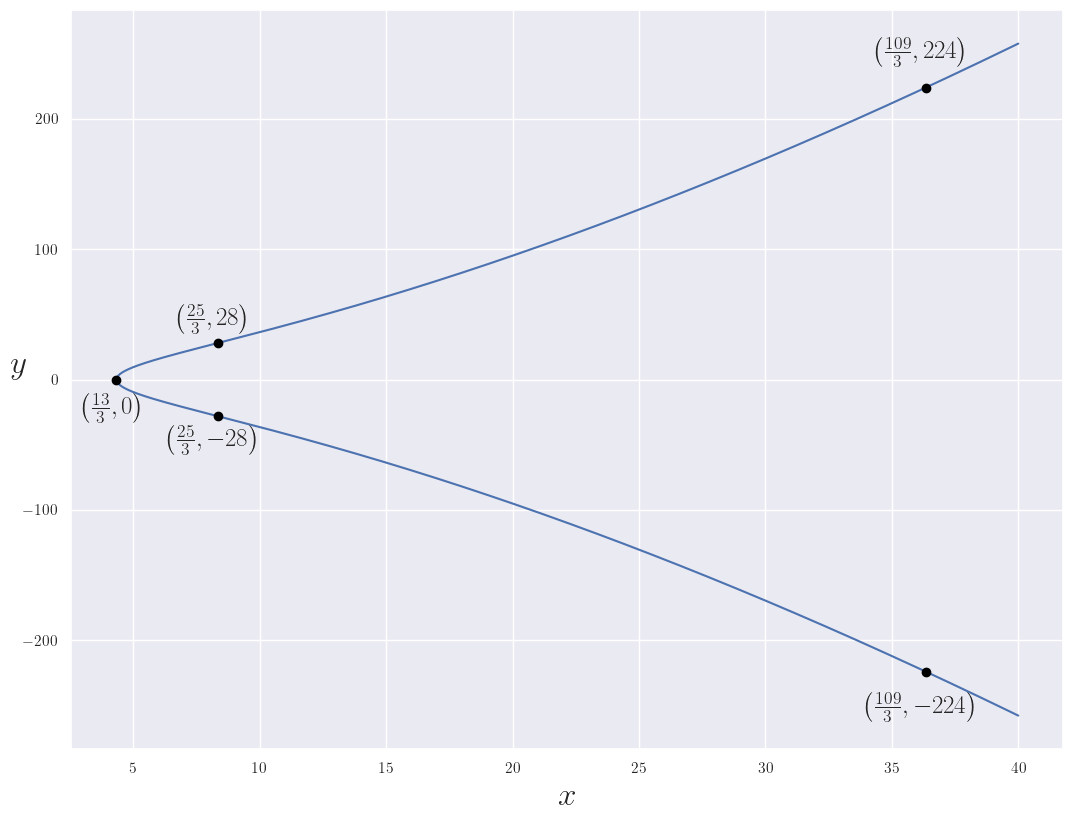
we find that there are only six rational points on the curve (including the point at infinity, which requires looking for points in projective space). These points are isomorphic to under addition on the curve, so a single generator is enough to describe the points. Using projective coordinates we can start with one of the two generators:
Since we'd like to convert these back to solutions we want to represent these points in terms of . Plugging in our transformations for and we have
These are relevant because we can convert to points in projective space using :
So unfortunately, half of the six rational points on the elliptic curve correspond to points at infinity and the other half are invalid because or .
The Next Best Thing
So we can't find solutions over and it's pretty obvious that we can find solutions over but is there anything simpler? What about over for a sufficiently small value of ? Luckily, we can search for solutions in these rings by slightly modifying our previous procedure to find rational solutions to
and can use a family of Möbius transformations to transform to Weierstrass form:
For all choices of there is a rational point that will always have order two and will always correspond to the invalid .
To find some solution over the "simplest" choice would be but it turns out the elliptic curve produced has even fewer rational points than the case! The rational points are isomorphic to and they correspond to a point at infinity and the point common to all values of .
The next choice up — — luckily yields an infinite family of rational points! The group has the same generator with finite order mentioned above and a second generator with infinite order . Following our transformation backwards from this point we get
To clear denominators we can arbitrarily choose and find a solution to the original equation:
It should come as no surprise that and are conjugates in .
The End
Even simple questions have deeper questions just one or two hops away! The offhand comment by SyberMath spawned an exploration that led to much deeper mathematics. In fact, the questions don't stop here. Clearly the differences between and above is part of a larger pattern and investigating that pattern more could lead to even more deep mathematics.
Given how simple the original homogeneous equation is, I was floored that there are zero rational solutions. But I was also ecstatic that the tools exist to conclusively confirm the absence of rational solutions. If you've made it this far, thanks for following along!
- I also really enjoy Michael Penn videos. ↩
- I actually consulted my great friend Wade when wading into these deep waters. ↩
- I have swapped out the variable names used in the video since I'll be introducing many more variables in this post. ↩