This is the second (continued from Part 1) in a series of three blog posts. In the following we'll investigate a few properties of an object called Conway's topograph. John Conway conjured up a way to understand a binary quadratic form – a very important algebraic object – in a geometric context. This is by no means original work, just my interpretation of some key points from his The Sensual (Quadratic) Form that I'll need for some other posts.

---

In the following, as mentioned in Part 1,

when referring to a base/superbase, we are referring to the lax equivalent of these notions.

To begin to form the topograph, note each superbase $\left\{e_1, e_2, e_3\right\}$ contains only three bases

as subsets. Going the other direction, a base $\left\{e_1, e_2\right\}$ can only possibly be contained as a subset of two superbases:

With these two facts in hand, we can begin to form the geometric structure of the topograph. The interactions between bases and superbases (as well as the individual vectors themselves) give us the form. In the graph, we join each superbase $(\bigcirc)$ to the three bases $(\square)$ in it.

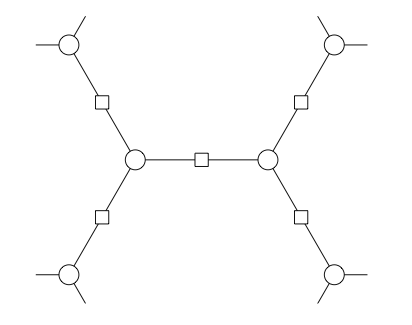
Each edge connecting two superbases $(\bigcirc)$ represents a base and we mark each of these edges with a $(\square)$ in the middle. Since each base can only be in two superbases, we have well-defined endpoints for each base (edge). Similarly, since each superbase contains three bases as subsets, each superbase (endpoint) has three bases (edges) coming out of it.

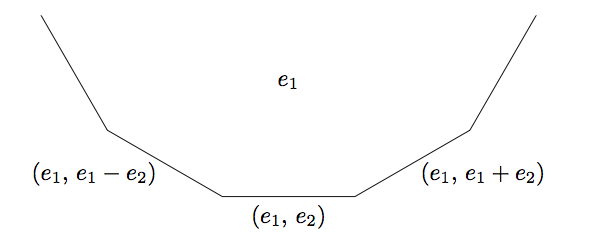
As we traverse each edge (base) surrounding a given vector $(e_1),$ we move from superbase (vertex) to superbase (vertex), and form a face. Starting from a base $e_1, e_2,$ traveling along each of the new faces encountered we begin to form the full (labeled) topograph below:

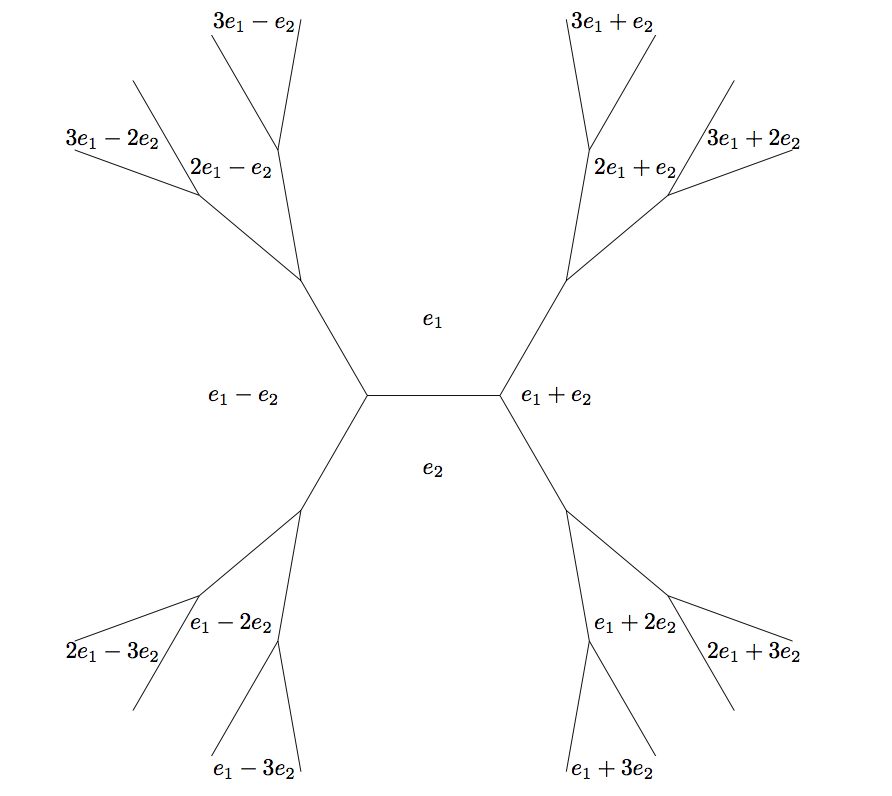
Notice the values of $f$ on the combinations of $e_1$ and $e_2$ is immaterial to the above discussion, hence the shape of the topograph doesn't depend on $f$.

If we know the values of $f$ at some superbase, it is actually possible to find the values of $f$ at vectors (faces) we encounter on the topograph without actually knowing $f$.

Claim:

For vectors $v_1, v_2,$

Proof:

Exercise. (If you really can't get it, let me know in the comments.) $\blacksquare$

This implies that if

then

form an arithmetic progression with common difference $h$. This so-called Arithmetic Progression Rule allows us to mark each edge with a direction based on the value of $h$. Hence if $d < a + b < c,$ we have $h > 0$ and the following directed edge:

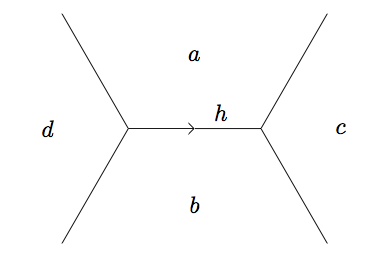
Obviously starting from a base $e_1, e_2,$ one wonders if it is possible to move to any pair $(x, y)$ with $x$ and $y$ coprime along the topograph. It turns out that we can; the topograph forms a structure called a tree, and all nodes are connected.

Lemma: (Climbing Lemma)

Given a superbase $Q$ with the surrounding faces taking values $a,$ $b,$ and $c$ as below, if $a,$ $b$ and the common difference $h$ are all positive, then $c$ is positive and the other two edges at $Q$ point away from $Q$.

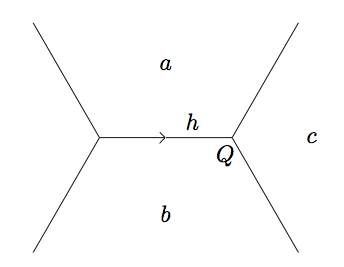
Proof:

First, $c$ is positive because $h = c - (a + b),$ hence $c = a + b + h > 0$. The two other edges at $Q$ have common differences $(a + c) - b$ and $(b + c) - a$. Since $c = a + b + h$ is greater than both $a$ and $b,$ these differences are positive. $\blacksquare$

Notice also that this establishes two new triples $(a, a + b + h, 2 a + h)$ and $(b, a + b + h, 2 b + h)$ that continue to point away from each successive superbase and hence climb the topograph. We can use this lemma (along with a specific form) to show that there are no cycles in the topograph, i.e. the topograph doesn't loop back on itself.

Consider the form which takes the following values at a given superbase:

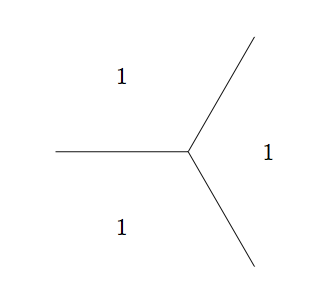
Due to the symmetry, we may consider traveling along an edge in any direction from this superbase identically. Picking an arbitrary direction, we reach the following superbase:

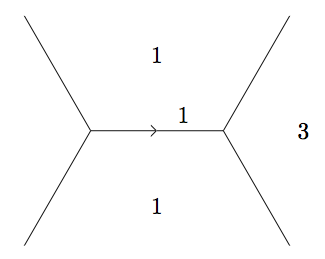
Since the values must increase indefinitely as laid out by the climbing lemma, the form can't loop back on itself; if it were to, it would need to loop back to a smaller value. Since this holds in all directions from the original well, there are no cycles.

Follow along to Part 3.

Update 1:

This material is intentionally aimed at an intermediate (think college freshman/high school senior) audience. One can go deeper with it, and I'd love to get more technical off the post.

Update 2:

All images were created with the tikz LaTeX library and can be compiled with native LaTeX if pgf is installed.