This is the second (continued from Part 2) in a series of three blog posts. In the following we'll investigate a few properties of an object called Conway's topograph. John Conway conjured up a way to understand a binary quadratic form – a very important algebraic object – in a geometric context. This is by no means original work, just my interpretation of some key points from his The Sensual (Quadratic) Form that I'll need for some other posts.

---

Definition:

For the form $f(x, y) = a x^2 + h x y + b y^2,$ we define the discriminant as the value $ab - \left(\frac{1}{2}h\right)^2$. $\blacksquare$

The base $(1, 0)$ and $(0, 1)$ take values $a$ and $b$ on the form in the Definition above and are part of a sequence with common difference $h$. In fact, if we know the values $a',$ $b'$ and the difference $h'$ at any base (edge in the topograph), the value $a'b' - \left(\frac{1}{2}h'\right)^2$ is independent of the base and the direction (left or right) which determines the sign of $h'$ and hence equal to the discriminant. To see this, first note the sign of $h'$ is immaterial since it is squared. Also, consider the two other bases (edges) in the superbase. As in the proof of the climbing lemma, one base takes values $a' = a$ and $b' = a + b + h$ with common difference $h' = 2a + h$ which gives

Similarly the other base in the given superbase gives

Having showed that there are no cycles when starting from a given superbase, our work in understanding the topographis not complete. We haven't actually showed that we can get from one superbase to any other superbases within the topograph. To show this, we'll use the discriminant and the following.

Definition:

A superbase $W$ is called a well if all the edges at $W$ point away from $W$. $\blacksquare$

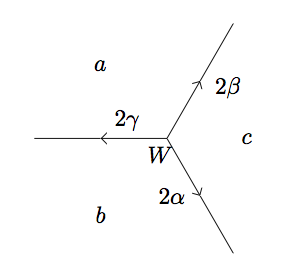
Notice a well is dependent on the values, hence depends on the form $f$. In a positive-valued topograph, we may find a well by traveling along the topograph in the opposite direction of the edges. Eventually, we must encounter a superbase where all arrows point out (as above), leaving us nowhere to travel and thus becoming our well. This is because, assuming the topograph is positive-valued, we can only decrease in value for so long (eventually the values must approach the minimum).

Lemma: (The Well Lemma)

For a positive-valued form $f$ and a well $W,$ the three values $f$ takes on the faces in $W$ are the smallest values that $f$ takes on the topograph.

Proof:

Using the labels from the well in the definition above, the Arithmetic Progression Rule for our differences gives

and solving,

Let the superbase $W = \left\{e_1, e_2, e_3\right\}$. Since $W$ is a superbase, we may write any vector as

for $m_1,$ $m_2,$ $m_3 \in \mathbf{Z}$. Also due to the fact that $W$ is a superbase, $e_1 + e_2 + e_3 = (0, 0)$ and so we may also write

for $k \in \mathbf{Z}$. From this it is clear only the differences of the $m_i$ matter. With this as our inspiration we write

a formula discovered by Selling.

To verify this, notice both sides of the equation are quadratic forms in $v$ and

hence they must be equal since both sides are quadratics that agree on more than two points.

If two of the $m_i$ are equal, then $v$ must be an integral multiple of the third vector, hence the value $f(v)$ will be at least as largeas the value of $f$ on the third vector. If not, all the differences must be nonzero (hence greater than or equal to $1$ in absolute value, since integers), thus

which is greater than or equal to each of $a = \beta + \gamma,$ $b = \alpha + \gamma,$ and $c = \beta + \alpha$ since all of $\alpha,$ $\beta,$ and $\gamma$ are non-negative. $\blacksquare$

Corollary:

The topograph is connected; one may travel along the topograph from any given superbase to any other.

Proof:

Using the same quadratic form $f$ as we did to show the topograph had no cycles, we can show it is connected. Any arbitrary superbase is on the topograph, hence must be in some connected component of the topograph, but there may be more than one component. Since $f$ is positive-valued, we must have some well in this component. But, by the above, the values at a well must be the absolute lowest values $f$ takes on the topograph. This implies the well must take the values $1,$ $1,$ $1$ and shows all superbases must be in the same component. $\blacksquare$

From this point, we will concentrate on a special type of form relevant to our discussion. For a form $f$ which takes both positive and negative values, but never $0,$ the topograph has a special path thatseparates the which separates the faces where takes a positive value and those where $f$ takes a negative value.

Claim:

If a form $f$ takes both positive and negative values, but not zero, then there is a unique path of connected edges separating the positive and negative values. What's more, the values that occur on this river do so periodically.

Proof:

Since the topograph is connected, there must be some edge where positive and negative values meet. As we proceed along adjacent edges, we can choose to follow a path of edges which will separate positive and negative (each subsequent value must be positive or negative, allowing us to "turn" left or right).

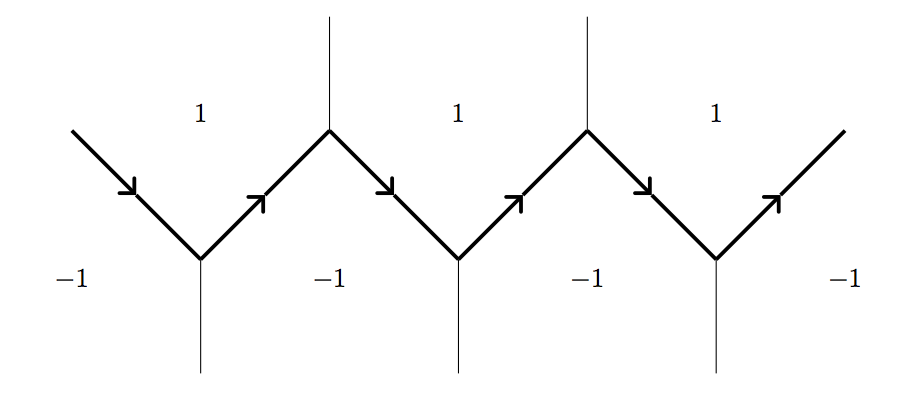
On first sight, there is no reason that this path should be unique. However, with the climbing lemma in mind, starting on the positive side of the path and moving away from the negative values, we must have only positive values. Using the logic of the climbing lemma instead with negative values, we similarly see that starting on the negative side and more away from the positive values will yield all negative numbers below the path. Hence nowhere above the path can positive and negative values meet and similarly below. Thus the path must be unique.

To show this path is periodic, we must utilize the discriminant. For each edge along the path, we have some positive value $a$ and a negative $b$ (by definition of the path) and the common difference $h$. Thus the determinant $D$ must be negative since the product $ab$ is, hence

Thus, both $\left(\frac{1}{2}h\right)^2$ and $\left|ab\right|$ are bounded by $\left|D\right|$. So $a,$ $b$ and $h$ are bounded by $\left|D\right|$. Thus we have finitely many possible triples $(a, b, h),$ hence some value must be repeated in the path. This forces the path to be periodic since the triple starting from one triple $(a, b, h)$ determines next triple along the path and hence the entire path.

This path is so crucial that we give it it's own name.

Definition:

If a form $f$ takes both positive and negative values, but not zero, we call the path separating the positive and negative values the river. $\blacksquare$

Thanks for reading, I'll make use of all this in a few days!

Update 1:

This material is intentionally aimed at an intermediate (think college freshman/high school senior) audience. One can go deeper with it, and I'd love to get more technical off the post.

Update 2:

All images were created with the tikz LaTeX library and can be compiled with native LaTeX if pgf is installed.